深入解析比特币中的离散函数:加密与安全的基石

在数字货币的世界中,比特币作为首个成功的加密货币,其背后的技术原理一直是人们关注的焦点。其中,离散函数作为比特币加密算法的核心组成部分,扮演着至关重要的角色。本文将深入解析比特币中的离散函数,探讨其在加密和安全方面的应用。
一、什么是离散函数?
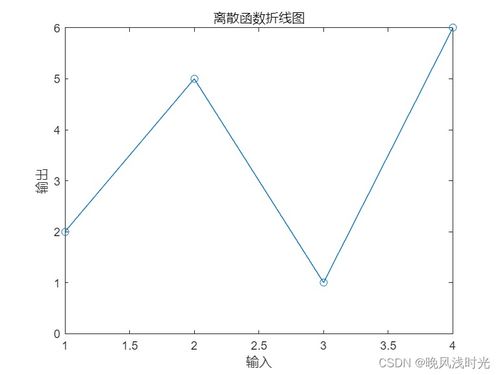
离散函数,顾名思义,是一种在离散数学领域广泛应用的函数。在密码学中,离散函数通常指的是一种将输入映射到输出,且输出具有唯一性的函数。这种函数的特点是单向性,即给定输出,很难找到对应的输入。
二、比特币中的离散函数:椭圆曲线离散对数问题
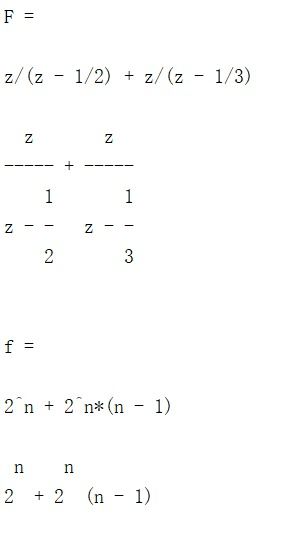
比特币的加密算法主要基于椭圆曲线离散对数问题(ECDLP)。椭圆曲线是一种特殊的数学曲线,其上的点满足特定的数学关系。在比特币中,椭圆曲线离散对数问题指的是:给定椭圆曲线上的一个点P和它的k倍点Q,找到整数k的过程。
由于椭圆曲线离散对数问题的困难性,使得比特币的加密算法具有较高的安全性。目前,还没有找到在多项式时间内解决ECDLP问题的算法,这使得比特币的加密算法在理论上被认为是安全的。
三、离散函数在比特币中的应用

1. 地址生成:比特币地址是用户进行交易时使用的唯一标识。通过椭圆曲线离散对数问题,可以将用户的私钥映射到一个公钥,进而生成一个比特币地址。
2. 交易签名:在比特币交易中,用户需要对自己的交易进行签名,以证明交易的有效性。通过椭圆曲线离散对数问题,用户可以使用自己的私钥对交易进行签名,确保交易的安全性。
3. 钱包安全性:比特币钱包的安全性依赖于私钥的保护。私钥是用户进行交易的关键,一旦私钥泄露,用户的资产将面临被盗的风险。离散函数的应用使得私钥的生成和存储更加安全。
离散函数作为比特币加密算法的核心组成部分,在保证比特币安全方面发挥着重要作用。通过对椭圆曲线离散对数问题的研究,我们可以更好地理解比特币的加密原理,从而为数字货币的发展提供理论支持。
随着数字货币的普及,离散函数在加密和安全领域的应用将越来越广泛。未来,随着密码学研究的不断深入,离散函数将在数字货币、区块链等领域发挥更大的作用。
